大学受験・入試情報

大学入学共通テストの数学の対策は？出題範囲やタイプ別勉強法を紹介

最終更新日：2023-05-29

「大学入学共通テスト」は、2021年から開始された大学入学を希望する受験生を対象とした試験です。大学入学共通テストの数学について、まだ傾向がつかめず、「どんな問題が出るの？」「どのような対策をしたらいいの？」と不安に思う受験生も多いのではないでしょうか。長文の問題が多く難しそうに思えますが、基礎をきっちり固め、対策・戦略を押さえて勉強すれば、高得点を狙うことも十分可能です。そこで本記事では、大学入学共通テストの数学の出題内容や難度、大学入試センター試験との違い、対策スケジュールのほか、タイプ別の勉強法と注意点について解説します。

この記事の目次

大学入学共通テストは高校の学習の達成度を判定する試験
大学入学共通テストの数学の出題内容
大学入学共通テストの数学の難度
大学入学共通テストと大学入試センター試験の数学の違い
学習指導要領変更に伴う2025年の共通テストの変更
大学入学共通テストの数学の対策スケジュール
タイプ別・大学入学共通テストの勉強法と注意点
- 6割の点数を目指すタイプ
- 8割以上の点数を目指すタイプ
大学入学共通テストの数学の対策
大学入学共通テストの数学こそ大学受験ディアロの「アウトプット学習」で対策しよう
■監修

大学入学共通テストは高校の学習の達成度を判定する試験

2021年から開始された大学入学共通テスト（以下、共通テスト）は、高校の基礎学習の達成度を判定するものであり、多くの国公立大学の合否判定の判断材料となります。共通テストは毎年1月中旬の土曜・日曜の2日間に、全国で一斉に実施され、2023年実施試験の志願者は約51万人でした。高校生の約2人に1人が受験する、日本の大学入試で最も規模の大きい試験です。

近年は、私立大学でも「共通テスト利用入試」を採用し、共通テストの結果を合否判定に用いる大学が増えています。共通テストを一度受験するだけで、複数の大学・学部に出願できることから、多くの受験生が利用しています。

共通テストの前身である大学入試センター試験（以下、センター試験）は、1990年から2020年まで30年間実施されました。共通テストはセンター試験よりも「思考力」「判断力」「表現力」を重視する内容に変わり、公式や解法などの丸暗記では、正答に結びつきにくい問題が多くなっています。

大学入学共通テストの数学の出題内容

共通テストの数学では、どのような問題が出題されるのでしょうか。ここでは、共通テスト「数学I・数学A」「数学II・数学B」の実施日と出題形式、問題構成を紹介します。

＞共通テストの数学対策なら大学入試専門塾の「ディアロ」。無料の学習相談受付中！詳細はこちら

実施日

数学の試験は、共通テスト2日目に実施されます。試験時間は例年、下記のスケジュールで、解答時間は「数学I」「数学I・数学A」が70分、「数学II」「数学II・数学B」が60分、いずれも配点は100点です。

■共通テストの数学の実施内容

試験時間	教科	解答時間	配点
11：20～12：30	数学1 「数学I」「数学I・数学A」	70分	100点
13：50～4：50	数学2（※）「数学II」「数学II・数学B」	60分	100点

※数学2には、ほかに「簿記・会計」「情報関係基礎」も含まれます。

出題形式

共通テストの数学は、全問マークシート方式です。計算して数字そのものをマークシートに記入する場合と、選択肢から選んで記入する場合の2パターンがあります。
例として、2022年実施試験の問題を見てみましょう。下記のように、「ア」「イ」「ウ」には計算から求められる数字をマークシートにそれぞれ記入し、「エ」には提示された解答群（選択肢）の中からひとつ選んで記入します。
マークシート方式は、塗り間違いに注意が必要です。特に、計算した数字をそのままマークするときには、塗り間違えないように見直してください。

■2022年実施試験「数学II・数学B」の本試験問題（抜粋）

出典：独立行政法人大学入試センター「令和4年度本試験の問題数学II・数学B」（2022年1月）（https://www.dnc.ac.jp/albums/abm.php?d=67&f=abm00000837.pdf&n=R4%E5%95%8F%E9%A1%8C_%E5%95%8F%E9%A1%8C_%E6%95%B0%E5%AD%A6%E2%85%A1%E3%83%BB%E6%95%B0%E5%AD%A6%EF%BC%A2.pdf)

問題構成

共通テストの数学では、「数学I・数学A」「数学II・数学B」ともに、第1問・第2問が必須問題、第3～5問は、2問を選択して解答します。
2023年実施試験の「数学I・数学A」「数学II・数学B」の問題構成や配点、出題分野は下記のとおりです。出題分野は実施年によって異なるため、幅広く学習しておく必要があります。

■2023年実施試験「数学I・数学A」の問題構成

大問	必答／選択	配点	出題分野
第1問	必答	30	（1）数と式（2）図形と計量
第2問	必答	30	（1）データの分析（2）二次関数
第3問	2問選択	20	場合の数と確率
第4問		20	整数の性質
第5問		20	図形の性質

■2023年実施試験「数学II・数学B」の問題構成

大問	必答／選択	配点	出題分野
第1問	必答	30	（1）三角関数（2）指数関数・対数関数
第2問	必答	30	（1）微分法（2）積分法
第3問	2問選択	20	確率分布と統計的な推測
第4問		20	数列
第5問		20	ベクトル

大学入学共通テストの数学の難度

共通テストの数学は、どのくらい難しいのでしょうか。下記のとおり、最後のセンター試験である2020年実施試験の平均点と比較すると、2021年実施の共通テストでは平均点が上がりました。しかし、2022年実施試験は「数学I・数学A」「数学II・数学B」ともに大幅に平均点が下がり、難度が上昇しています。
2023年実施試験の最終集計（2023年2月6日発表）では、2022年実施分に比べると平均点は上がり、比較的やさしかったようです。

■共通テストとセンター試験の数学の平均点

科目	満点	2023年実施分平均点（最終集計）	2022年実施分平均点	2021年実施分平均点	2020年実施分平均点（センター試験）
数学I	100	37.84	21.89	39.11	35.93
数学I・数学A	100	55.65	37.96	57.68	51.88
数学II	100	37.65	34.41	39.51	28.38
数学II・数学B	100	61.48	43.06	59.93	49.03

2020年実施のセンター試験と比べると、2023年実施の共通テストの難度は下がっているように見えますが、1問あたりに読む文章量が多く、決して簡単ではありません。長文から必要な情報をピックアップする「読解力」や解法を導く「思考力」、時間内に解答する「スピード」が必要です。
また、共通テストは日常的な物事を数学的に検討したり、会話の誘導文に沿って解答したりといった独特の問題があります。これらの問題は、公式や定理、解法を丸暗記しただけでは正答につながりにくく、公式をどこでどのように使うか、なぜこの定理なのかなど、根本的な意味を理解することが重要です。また、題材は多種多様で、どのテーマでも読解できるよう、幅広い知識を身につける必要があります。
とはいえ、問題に必要とされる公式や定理そのものは基本的なものばかりで、典型的なパターンの出題が多いです。特殊な知識ではなく、あくまで基礎知識が重要となります。つまり、共通テストの数学では、問題文で問われた内容を理解して基本的な知識を応用する、問題解決能力が求められるでしょう。

大学入学共通テストと大学入試センター試験の数学の違い

30年間実施されたセンター試験に変わり、2021年から導入されたのが共通テストです。この2つの数学の問題には、どのような違いがあるのでしょうか。

出題形式

センター試験では、ほとんどの問題が計算の解そのものをマークして回答する形式でした。共通テストでも同じ形式の問題はありますが、選択肢の中から解答を選ぶ問題が増えています。選択肢は、多いときには10個あることもあり、さらに選択肢が文章になっている場合もあります。
また、共通テストは全体的に問題文の文章量が増え、「数学I・数学A」「数学II・数学B」ともに4割程度、問題のページ数が増えました。つまり、センター試験に比べると、より読解力とそのスピードが求められるということです。
共通テストの数学で特徴的な問題には、下記の2つが挙げられます。

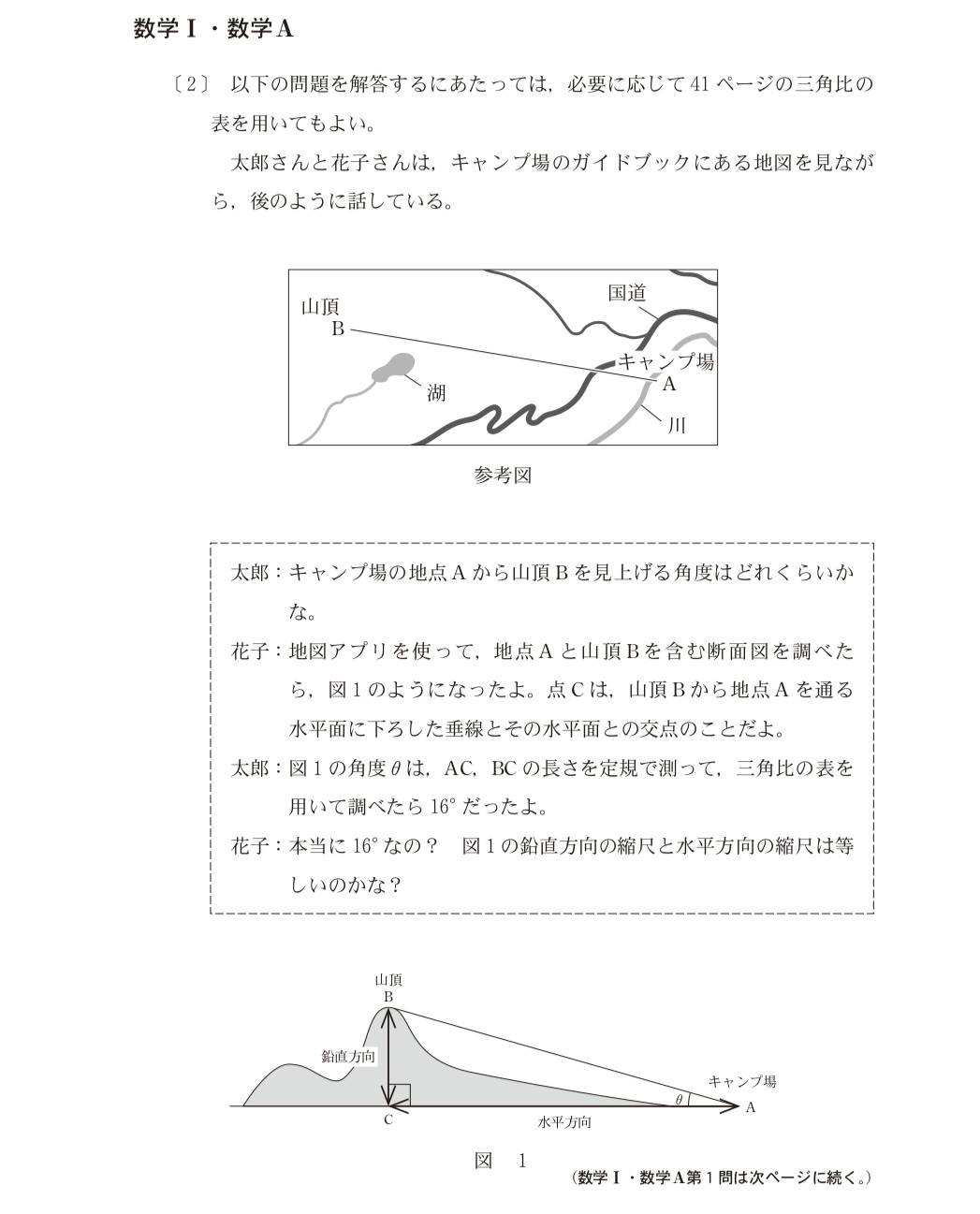
日常的な物事を数学的に検討する問題

共通テストの数学には、地図やスポーツなど、日常的なテーマの文章や図を読み取って解答する問題があります。下記のように、テーマの提示が長文のため、何を問われているのかを短時間で把握することが求められます。共通テスト以外でこのような問題はあまり見られないため、過去問などで共通テスト形式に慣れておくことが重要です。

■2022年実施試験「数学I・数学A」の本試験問題（抜粋）

出典：独立行政法人大学入試センター「令和4年度本試験の問題数学I・数学A」（2022年1月）（https://www.dnc.ac.jp/albums/abm.php?d=67&f=abm00000838.pdf&n=R4%E5%95%8F%E9%A1%8C_%E5%95%8F%E9%A1%8C_%E6%95%B0%E5%AD%A6%E2%85%A0%E3%83%BB%E6%95%B0%E5%AD%A6%EF%BC%A1.pdf）

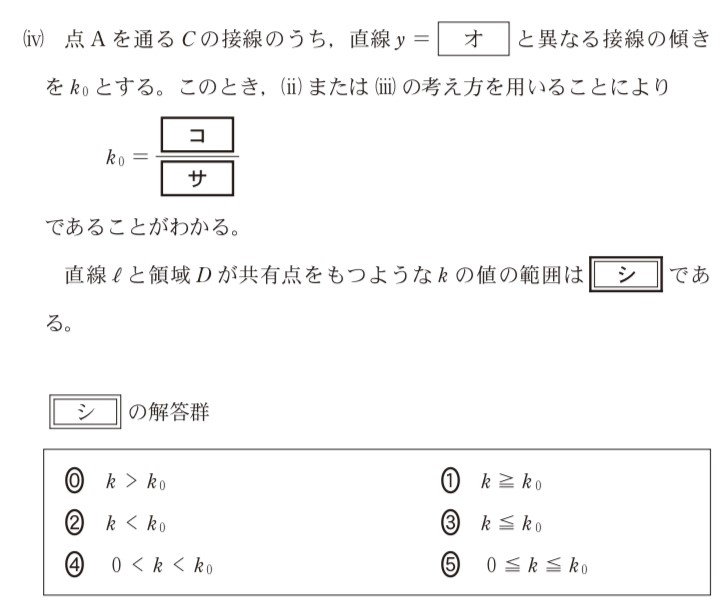
学生2人の会話から計算を導く問題

学生2人による数学の問題についての会話を読み、穴埋め方式で解答していく問題もあります。下記のように、計算の解答方法を検討する会話に沿って解答するため、計算問題を解く「過程」を意識した準備が必要でしょう。

■2022年実施試験「数学I・数学A」の本試験問題（抜粋）

問題構成

問題構成は、センター試験から変更はありません。「数学I・数学A」「数学II・数学B」ともに、第1問・第2問が必答で、第3～5問から2問選択します。

配点

配点も、センター試験と変わりません。「数学I・数学A」「数学II・数学B」ともに、必答の第1問・第2問が各30点、選択問題の第3～5問は2問選択で各20点、満点は100点です。

試験時間

「数学I・数学A」は、センター試験では60分でしたが、共通テストでは70分になりました。センター試験から10分増えましたが、同時に長文の問題が増えているため、時間に余裕があるわけではないでしょう。
また、「数学II・数学B」は60分でセンター試験と変更はありません。しかし、「数学I・数学A」同様、長文問題が増えており、従来に比べて時間に余裕がなくなったと感じる可能性もあります。
「数学I・数学A」「数学II・数学B」いずれも時間配分をあらかじめ決め、時間内に確実に目標点が取れるようにすることが重要です。

学習指導要領変更に伴う2025年の共通テストの変更

学習指導要領が、2022年度（2022年4月）の高校入学者から変更されました。学習指導要領とは、教科やその教育内容などを定めたカリキュラムのこと。つまり、2022年4月に入学した高校1年生から、学校で学ぶ教科（科目）や学習内容が変わったということです。
そのため、2022年度高校入学者が大学入試に臨む2025年の共通テストでは、新学習指導要領に合わせた試験内容になります。詳細は下記を参考にしてください。

■新学習指導要領での変更点

教科	グループ	2024年まで	2025年から
国語		「国語」	「国語」
地理歴史		「世界史A」「世界史B」「日本史A」「日本史B」「地理A」「地理B」	「地理総合、地理探究」「歴史総合、日本史探究」「歴史総合、世界史探究」「地理総合、歴史総合、公共」「公共、倫理」「公共、政治・経済」
公民		「現代社会」「倫理」「政治・経済」「倫理政治・経済」
数学	数学（1）	「数学I」「数学I・数学A」	「数学I」「数学I・数学A」
数学	数学（2）	「数学II」「数学II・数学B」「簿記・会計」「情報関係基礎」	「数学II、数学B、数学C」
理科	理科（1）	「物理基礎」「化学基礎」「生物基礎」「地学基礎」	「物理基礎」「化学基礎」「生物基礎」「地学基礎」
理科	理科（2）	「物理」「化学」「生物」「地学」	「物理」「化学」「生物」「地学」
外国語		「英語」「ドイツ語」「フランス語」「中国語」「韓国語」	「英語」「ドイツ語」「フランス語」「中国語」「韓国語」
情報		–	情報I

出典：文部科学省「新学習指導要領に対応した令和6年度に実施する大学入学共通テストの出題教科・科目について」（2022年3月）（https://www.mext.go.jp/content/20210621-mxt_daigakuc02-000016052_9.pdf）

数学は、学習指導要領に新しく「数学C」が設置され、従来は「数学II」「数学II・数学B」「簿記・会計」「情報関係基礎」から1科目選択でしたが、「数学II、数学B、数学C」のみになります。
「数学C」とは、従来の「数学B」の「ベクトル」、「数学III」の「平面上の曲線と平素数平面」で構成された科目のこと。2025年1月実施の共通テストから、「数学II、数学B、数学C」の選択問題は、下記4項目から3項目を選ぶことになります。

■「数学II、数学B、数学C」選択問題（3項目選択）

・数学B：数列
・数学B：統計
・数学C：ベクトル
・数学C：平面上の曲線と平素数平面

従来よりも出題範囲が広くなることから、どの単元をどのように対策していくか、今まで以上にしっかりしたリサーチと作戦立てが必要になるでしょう。

大学入学共通テストの数学の対策スケジュール

共通テスト数学で高得点を狙うためのスケジュールとしては、

【高3・1学期】基礎力の強化
↓
【高3・夏休み】問題形式の対策
↓
【高3・2学期～】実戦演習

と、共通テストまでの9ヵ月を、3つの期間で区切るのがおすすめです。

ここでは、高校3年生の期間ごとの勉強のコツを紹介します。

【高3・1学期】基礎力強化

1学期は、数学的な基礎力をつけることを目標に、定理・公式などの知識や解法を学び、基本問題を解きます。ポイントは、この段階で苦手分野を残さないことにあります。共通テストの数学は「広く、浅く」すべての分野から出題されるからです。試験本番で焦らないためにも、基礎である公式や定理、解法をしっかりインプットし、本番で使えるようにしておいてください。
また同時に、数学の基本的な概念や定義・定理を十分に理解し、自分の言葉で説明できるようにすることも重要です。公式だけを知っていればいいのではなく、公式の成り立ちまで説明できると、共通テストの数学では強みになります。特に集合と論証、図形の証明、確率やデータの分析などで、この傾向が顕著です。

共通テストの対策においては、「第3～5問の選択問題の単元であらかじめ受けるものを決めて、選ばない単元は勉強しない」という考えも必要です。数学が苦手な人の場合、無理をして網羅的に勉強しようとするより、確実に得点を確保しようとする勉強のほうが、結果的に得点につながることもあるからです。
また、2025年の共通テストでは「数学II、数学B」に「数学C」が加わります。「数学C」をどのように勉強するかは、国公立大学や私立大学の入試をどう受けていくかという戦略自体にかかわってくるでしょう。

【高3・夏休み】共通テスト形式の対策

夏休みは、共通テストの出題形式に慣れるため、試行調査の問題や予想問題、センター試験の過去問などを実際に解いてみてください。共通テストは「答えの数値をマークする」「選択肢の番号をマークする」「適するものをすべてマークする」などマーク方法もさまざまです。マークミスがないように注意を払いましょう。
また、共通テストには解答プロセスに沿って解いていく問題もあり、慣れていないと解答に時間がかかることがあります。夏休みの期間中に、できるだけ多く共通テスト形式の問題で練習しておきましょう。

【高3・2学期～】実戦演習

2学期に入ったら実戦あるのみです。現役生の勉強の成果が現れるには、時間がかかります。始めにあまり得点できなくても、焦らなくて大丈夫です。実践と弱点補強を繰り返す中で、冷静に原因を見つけ、基本を見直します。
数学は、「試験時間が足りない」という声が多い教科でもあります。大問ごとの時間配分をあらかじめ決めておく、計算方法を工夫するなど、時間内に全問解ききることを心掛けましょう。

また、選択問題の第3～5問では、試験が開始されてから解くべき問題を見極める力が必要です。ある程度どの問題を解くかを定めていても、出題の難度によっては違う問題を選択せざるをえない場合もあります。
点数が取れない問題は「選択しない」のも戦略のひとつです。すぐに決められない場合に備えて、「◯分考えて解答できなければほかの問題に取り組む」といった自分のルールを決めておくと、時間を効率的に使えます。

文系や中堅大学の理系学部を受験する場合には、上記の対策スケジュールで問題ありません。しかし、難関大学の理系学部を受験する場合は、高校3年生の夏までに共通テストの実践演習までの対策が終わっていることが理想です。
高校によっては、上記の対策スケジュールよりも授業の進度が遅いこともあります。その場合には、学校の授業より早めに共通テストの対策をする必要があるため、塾を活用したり意識的に参考書や問題集で先に勉強を進めたりする必要があります。

タイプ別・大学入学共通テストの勉強法と注意点

共通テストの対策は、どのくらいの点数を取りたいかによって変わります。中堅大学を志望して、数学で「6割」の点数を目指すタイプと、難関大学を志望して「8割以上」の点数を目指すタイプの勉強法と注意点をご紹介します。

6割の点数を目指すタイプ

共通テストの数学で6割を目指すには、どの分野も満遍なく反復練習し、確実に基礎をインプットすることが重要です。計算の基礎ができていること、苦手分野を作らないことは欠かせません。

問題集を1冊決めて、繰り返し徹底的に問題を解いていくといいでしょう。1回目は、解けた問題に「◯」、解けなかった問題に「×」をつけます。2回目は、「×」の問題を優先的に解いて、すべて「◯」になったら、3回目は「◯」「×」に関係なく問題を解いていくのです。このように、間違えやすい問題や、苦手意識のある問題を繰り返し解くことで、確実に学力をアップできます。

もちろん問題集でも、反復練習をすることで計算の基礎を培うことはできます。しかし、さらに効率的に基礎を習得するには、AIトレーニングがおすすめです。
大学受験ディアロのAIトレーニングコース「atama＋（アタマプラス）」では、一人ひとりの理解度やミスの傾向などの学習状況をAIが分析し、最短・最適な学習計画を立てられます。「理解不足」をそのままにせず、反復練習で基礎力を確実につけられることから、受験生から「基礎の復習を網羅的にスピーディーに進められた」など、好評の声をいただいています。気になる人は、ぜひチェックしてみてください。

AIトレーニングコースの詳細は、下記のページで紹介しています。
AIトレーニングコースーアタマプラス/atama＋

8割以上の点数を目指すタイプ

難関大学の合格を目指すには、8割以上を目指す必要があります。このレベルになると、基礎が定着していることはもちろん、より高度な「読解力」と「思考力」が必要です。というのも、共通テストの問題は長文が多く、必要な情報から解答を導き出す必要があるからです。

過去問を解くときは問題文を読んでから図を書いたり頭でイメージしたりして、問題を解く練習をしてください。このとき、最初から「目標時間を設けて時間内に解く」のではなく、「時間無制限で目標点を確保する」ようにします。点が取れないのに解答スピードを上げたところで、あまり意味はありません。
時間無制限（ただし計測自体は実施）で確実に目標点を取れるようになってから、目標時間を段階的に縮め、最終的には共通テスト本番の時間内に目標点を確保できるようにする勉強法が効果的です。
共通テストは、奇抜な発想力が必要とされる試験ではありません。基礎を重視しながらも、読解力・思考力を必要とすることで難しくなっているといえます。応用的な問題で正答するためには、ただ「問題を解き、答え合わせをする」だけでは不十分です。常に解答にいたる道のりを論理的に説明できるようにしてください。その上で、ひとつのパターンをさまざまな設問に応用させることが必要なのです。

大学入学共通テストの数学の対策

共通テストの数学で高得点を取るためには、これから紹介する4つのステップで学習していくことが重要です。それぞれのステップで注意すべきことやコツをご紹介しますので、ぜひ参考にしてください。

1. インプット学習

まずは、全分野の基本的な公式を暗記することから始めましょう。ただ覚えるだけでなく、基本的な問題で公式を使って解答できるよう、反復学習することが重要です。また、問題・解答にはパターンがあるため、典型的なパターンの解法を暗記することも有効です。同じような基礎問題で反復練習すると、基礎が定着していきます。
共通テストで時間内に確実に目標点を確保するには、時間配分が重要です。公式や典型的な解答パターンを覚えることで基礎的な問題は短時間で解けるようになり、その分、長文問題に時間を割けます。

2. アウトプット学習

次に、アウトプットをしていきますが、いきなり共通テストの過去問を解くことはあまりおすすめしません。基礎が定着しないまま共通テストに取り組んでも、解けずに焦りだけが募る可能性があります。
まずは、どのような問題でどの公式を使うのか、どのような問題で典型的な解答パターンが使えるのかを自分で考え、整理することが重要です。さらに、問題に対して「どうしてその公式を使うのか」「どうしてその解答パターンを使ったのか」を説明できるようになると、基礎が定着できるだけでなく、さまざまな応用問題に対して論理的に解答できるようになるでしょう。

しかし、1人で勉強していると問題を繰り返し解くことはできても、人に説明する機会は少ないかもしれません。大学受験ディアロでは、映像教材で知識を身につけ、学んだ内容をトレーナー（講師）に説明し、トレーナーからの質問に答えるという「反転学習」を採用しています。学んだことを人に説明（アウトプット）することで、より深く理解し確実に定着することが可能です。自宅でも受講できますので、ぜひチェックしてみてください。

反転学習の詳細は、下記のページで紹介しています。
1:1対話式トレーニングコース

3. 共通テストの形式に慣れる

基礎が定着したら、過去問などで共通テストの形式に慣れるようにしましょう。前述のように、本番のテストで全問解くには時間配分が重要です。計算問題を速く、正確に解答することで、長文の問題に時間を割けます。そこで、計算練習をしてスピードと正確性アップを目指すことから始めることがおすすめです。

また、文章から問題設定を的確に読み取り、図にしたり式を立てたりしながら、どのようなパターンに持っていけるかを考える必要があります。文章量が多い問題は慣れが必要なため、繰り返し練習が必要です。このとき、本番同様にマークシート形式で解答することや、余白の限られたスペースで計算することに慣れておくことも重要です。

4. 客観的な自己分析からの作戦立て

最後に、共通テストの問題で高得点を取るための戦略を立てます。過去問などを解いた結果から客観的に自己分析し、「大問ごとの時間配分」「目標点数」を具体的に設定し作戦を立てるのです。特に、時間配分は、あらかじめ決めておくことで解答に必要な時間がわかり、対策がしやすくなります。

また、得意な分野の問題であっても、計算ミスはよくあることです。計算ミスは「気をつける」だけでは減ることはなく、なくすこともできません。計算ミスをどうしたら防げるのかと、見直しにより計算ミスに気づく方法を考えておくと安心です。練習問題や模試などで、さまざまな方法を試してみてください。
さらに、現時点での自分の実力や苦手分野の傾向を把握し、分析・アドバイスをする相談相手がいると心強いものです。信頼できる高校の先生、塾の先生に相談してみるといいでしょう。

大学入学共通テストの数学こそ大学受験ディアロの「アウトプット学習」で対策しよう

大学入学共通テストの数学は、過去問に取り組むだけでは高得点は取れません。
基礎をインプット・アウトプットし、共通テスト形式に慣れ、同時に戦略を立てることが重要でしょう。また、試験までに得た知識や情報を活かして「読解力」と「思考力」を駆使し、問題を解けるかが重要であり、そのためには自分の言葉でアウトプットをする訓練が必要になります。もちろん、1人で共通テスト対策はできますが、自分の弱点は自分ではわかりにくいものです。

大学受験ディアロでは、映像教材による効率的なインプット学習と、学習内容をトレーナー（講師）に説明（アウトプット）し、トレーナーからの質問に答えるという反転学習の「1:1対話式トレーニングコース」が特徴です。自宅でも受講できますので、ぜひチェックしてみてください。
また、苦手分野がある人でも効率的な学力アップが目指せるAIトレーニングコース「atama＋（アタマプラス）」があれば安心です。

大学受験ディアロは、共通テストの数学で高得点を取りたい人の強い味方になるはずです。興味がある方はぜひ、教室見学や無料体験にお申し込みください。

教室見学・無料体験は、下記のページから。
教室見学・無料体験のお申込み

■監修

武田優士（たけだ・まさし）
株式会社ゼニスディアロ運営部課長兼指導開発課課長。大学受験領域を専門として、学習塾の運営に2002年から20年間携わる。以前は集団塾で教壇に立ち、授業・科目指導（英語）を担当したことも。現在は、ディアロのスクールを管轄するエリアマネージャーのほか、責任者として商品開発・公民事業・マーケティングに従事。